Life-Preference Constrained Loss (LPCL)

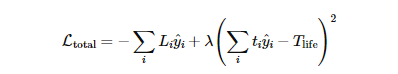
이 수식을 문장으로 다시 읽으면
“나는 좋아하는 것에 집중하도록 학습하되,
인생이라는 시간 제약을 어기지 않게 스스로를 훈련한다.”
1️⃣ 이 수식은 “무엇”인가?
한 줄 정의
이 수식은 “선택을 잘했는지 못했는지”를 숫자로 평가하는 기준이다.
AI 용어로:
- 손실 함수 (Loss Function)
- 최소화(minimize) 대상
값이 작을수록 좋은 선택
2️⃣ 왼쪽: L total
의미
- 전체 손실
- “지금 내 선택이 얼마나 아쉬운가?”
3️⃣ 수식은 크게 두 덩어리로 나뉜다
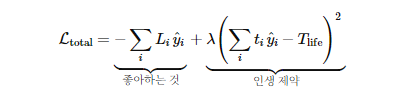
4️⃣ 첫 번째 항: 좋아하는 것에 대한 항
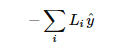
.
4-1. 기호 하나씩
| 기호 | 뜻 |
|---|---|
| " i " | 활동 번호 |
| " Li " | i번째 활동을 얼마나 좋아하는지 |
| " y^ " | 그 활동에 얼마나 집중하는지 |
| " ∑i " | 모든 활동을 다 더함 |
| " - " | 좋아할수록 손실이 줄어들게 함 |
4-2. 문장으로 읽으면
“내가 좋아하는 활동에 많이 집중할수록 손실은 작아진다.”
👉 좋아하는 것을 하면 보상, 하지만 손실 함수에서는 마이너스를 붙여서 줄어들게 만든다.
5️⃣ 두 번째 항: 인생은 짧다 (제약 조건)
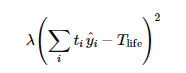
5-1. 기호 하나씩
| 기호 | 뜻 |
|---|---|
| ti | i번째 활동에 필요한 시간 |
| y^i | 그 활동에 쏟는 정도 |
| ∑i ti y^i | 내가 쓰는 총 시간 |
| Tlife | 내가 쓸 수 있는 전체 인생 시간 |
| (⋅)2 | 넘기면 강한 벌점 |
| lambda λ | 제약의 중요도 (엄격함) |
5-2. 문장으로 읽으면
“내가 쓰는 총 시간이 인생 시간을 초과하면 그 초과분을 제곱해서 강하게 벌점을 준다.”
PINN에서 PDE 오차 항과 동일한 역할
6️⃣ 왜 제곱이 들어가는가?

의미:
- 안 넘기면 → 거의 0
- 조금 넘기면 → 경고
- 많이 넘기면 → 폭발적인 벌점
“인생은 무리하면 안 된다”는 수학적 표현
7️⃣ λ lambda는 무엇인가?
한 줄 정의
현실을 얼마나 엄격하게 볼 것인가를 정하는 노브
| lambdaλ 값 | 인생 스타일 |
|---|---|
| 작음 | 하고 싶은 것 위주 |
| 큼 | 시간·현실 엄격 |
8️⃣ 전체 수식을 문장 하나로 읽기
“나는 좋아하는 것에 집중하려 하지만, 인생 시간이라는 한계를 넘기면
강한 벌점을 받도록 설계되어 있다.”
9️⃣ AI / PINN 관점에서 재정리
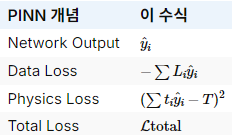
👉 완벽한 PINN 구조
🔟 마지막 한 줄 요약
“후회를 최소화하면서, 인생의 제약을 지키는 선택”을 수학으로 쓴 것이다.
나의 애정이 담긴 활동에 더 깊이 몰입할수록, 그리고 나의 시간이 삶의 목표와 완벽한 조화를 이룰수록, 인생의 후회(손실)는 사라진다.
가치 있는 일에 쏟는 에너지를 극대화하여 손실을 줄이되, 주어진 생애라는 시간의 한계를 벗어나지 않도록 삶의 균형을 맞추는 과정.
좋아하는 것들로 일상을 가득 채우는 일, 그리고 나에게 허락된 시간()을 남김없이 아름답게 사용하는 일. 그 두 가지가 만날 때 비로소 최소한의 손실을 가진 완벽한 삶이 완성된다.
문장 구성의 비밀 (수식과의 연결)
- "애정이 담긴 활동에 몰입": (값이 커질수록 전체 손실은 마이너스가 되어 작아짐)
- "삶의 목표와 조화/시간의 한계": (내 시간 합계가 목표치에 가까울수록 손실이 0이 됨)
- "손실은 작아진다": 의 최소화
박종영
대표이사
명
0개의 댓글
로그인
로그인 이후 댓글 쓰기가 가능합니다.
