지역 AX 산업 혁신의 메트로놈 효과

지역 AX 산업 혁신의 메트로놈 효과: 생태계 변화

					datalink(박종영) 

32개 메트로놈이 보여주는 혁신의 원리

나무 판자 위에 놓인 32개의 메트로놈이 각각 다른 리듬으로 시작하지만 시간이 지나면서 완벽하게 동조된 하나의 박자를 연주하게 되는 현상은 지역 AX 산업 혁신의 과정과 놀랍도록 유사합니다. 각 메트로놈이 미세한 진동을 통해 서로 영향을 주고받으며 자연스러운 조화를 이루어내듯, 지역 산업 생태계도 한 사람의 혁신적 활동이 만드는 '진동'을 통해 전체 시스템의 변화를 이끌어낼 수 있습니다.

혁신의 씨앗:  선한 영향력

지역 AX 산업의 혁신은 대부분 한 사람의 작은 실천에서 시작됩니다. 한 기업가가 새로운 기술을 도입하거나, 한 연구자가 혁신적인 아이디어를 제시하거나, 한 공무원이 규제 개선을 위해 노력하는 것처럼, 개인의 선한 의도와 실행력이 지역 전체의 변화를 촉발하는 첫 번째 메트로놈 역할을 합니다.

이러한 개인은 마치 첫 번째 메트로놈처럼 자신만의 고유한 리듬을 가지고 있지만, 동시에 주변 환경과 끊임없이 상호작용하며 미세한 변화의 신호를 보냅니다. 새로운 비즈니스 모델 도입, 기술 혁신 시도, 인재 육성 프로그램 운영, 지역 네트워크 구축 등의 활동이 바로 이러한 '진동'에 해당합니다.

상호작용을 통한 확산: 생태계의 형성

쿠라모토 모델에서 각 진동자가 다른 진동자들의 상태를 감지하고 영향을 받듯이, 지역 AX 산업 생태계에서도 한 주체의 혁신적 활동은 점차 다른 주체들에게 전파됩니다. 혁신적인 기업의 성공 사례를 본 다른 기업들이 유사한 기술 도입을 시도하고, 새로운 인재 양성 프로그램에 참여한 인력들이 각자의 직장에서 변화를 만들어내며, 성공적인 산학협력 모델을 경험한 대학과 연구기관들이 더 적극적인 협력 체계를 구축하게 됩니다.

이 과정에서 중요한 것은 각 주체들이 강제로 변화하는 것이 아니라, 서로의 성공과 노하우를 관찰하고 학습하면서 자발적으로 변화를 선택한다는 점입니다. 메트로놈들이 외부의 조작 없이 자연스럽게 동조되듯, 지역 산업 생태계의 각 구성원들도 서로의 긍정적 에너지와 성과에 영향을 받아 스스로 혁신에 참여하게 됩니다.

임계점 돌파: 생태계 전환의 순간

쿠라모토 모델에서 발견한 가장 중요한 통찰인 '임계점' 개념은 지역 AX 산업 혁신에서도 핵심적인 역할을 합니다. 충분한 수의 기업, 기관, 인력이 혁신 활동에 참여하기 시작하면, 지역 전체의 산업 생태계가 급격히 변화하는 순간이 옵니다. 이때 개별 주체들의 작은 변화들이 모여 지역 전체의 경쟁력 향상, 새로운 산업 클러스터 형성, 혁신 문화 정착 등의 큰 변화를 만들어냅니다.

예를 들어, 지역 내 몇 개의 기업이 디지털 전환에 성공하면서 생산성이 향상되고, 이를 본 다른 기업들이 연쇄적으로 디지털화에 참여하며, 관련 교육기관과 지원기관들이 전문 프로그램을 개발하고, 지방정부가 정책적 지원을 강화하면서 지역 전체가 스마트 제조업 허브로 변모하는 것과 같은 현상입니다.

자기 강화 메커니즘: 지속가능한 혁신 생태계

메트로놈들이 한번 동기화되면 그 상태를 자연스럽게 유지하듯, 지역 AX 산업 생태계도 임계점을 넘어서면 자기 강화 메커니즘이 작동합니다. 혁신적인 기업들이 늘어나면서 우수한 인재들이 지역으로 유입되고, 이들이 다시 새로운 기업을 창업하거나 기존 기업의 경쟁력을 높이며, 성공 사례들이 축적되면서 투자와 지원이 늘어나는 선순환 구조가 만들어집니다.

이러한 생태계에서는 새로 진입하는 기업이나 인력들도 자연스럽게 혁신적인 문화와 관행을 받아들이게 되며, 기존의 보수적이거나 소극적인 주체들도 점차 변화의 흐름에 동참하게 됩니다. 마치 새로 추가된 메트로놈이 이미 동조된 다른 메트로놈들의 리듬에 맞춰지듯, 생태계의 전반적인 혁신 분위기가 모든 구성원들을 같은 방향으로 이끌어가는 것입니다.

지역 AX 산업 혁신의 실천 방안

지역 AX 산업에서 메트로놈 효과를 만들어내기 위해서는 몇 가지 핵심 조건들이 필요합니다. 먼저 혁신의 첫 번째 메트로놈 역할을 할 선도 기업이나 개인이 있어야 하고, 이들의 성과와 노하우가 다른 주체들에게 효과적으로 전달될 수 있는 네트워크와 소통 채널이 구축되어야 합니다.

또한 각 주체들이 서로의 변화를 관찰하고 학습할 수 있는 기회가 많아야 하며, 혁신 시도에 대한 적절한 지원과 인센티브가 제공되어야 합니다. 실패에 대한 관용적 분위기와 재도전 기회 제공도 중요한 요소입니다.

무엇보다 중요한 것은 각 주체들의 자발적 참여를 이끌어내는 것입니다. 위에서 아래로의 강제적 변화보다는 성공 사례를 통한 동기 부여와 상호 학습을 통해 자연스러운 변화를 유도하는 것이 더욱 지속가능하고 효과적입니다.

작은 시작이 만드는 큰 변화

32개의 메트로놈이 만들어내는 완벽한 조화는 지역 AX 산업 혁신의 가능성을 보여줍니다. 한 사람의 작은 실천과 선한 영향력이 점차 확산되어 지역 전체의 산업 생태계를 변화시키고, 결국 지속가능한 혁신 시스템을 구축할 수 있다는 희망을 제시합니다.

오늘 한 기업가의 새로운 도전, 한 연구자의 혁신적 아이디어, 한 공무원의 개선 노력이 내일은 지역 전체의 산업 혁신으로 이어질 수 있습니다. 메트로놈의 동기화가 보여주듯, 개별의 작은 변화들이 모여 전체의 큰 조화를 만들어내는 것처럼, 우리 각자의 혁신적 실천이 모여 지역 AX 산업의 새로운 미래를 만들어갈 것입니다.

참고 자료: Synchronization of Metronomes & Kuramoto Model

메트로놈 동기화 현상 (Metronome Synchronization)

메트로놈 동기화는 1665년 네덜란드의 물리학자 크리스티안 하위헌스(Christiaan Huygens)가 처음 발견한 현상입니다. 그는 벽에 걸린 두 개의 진자시계가 처음에는 서로 다른 리듬으로 작동하다가 시간이 지나면서 같은 박자로 맞춰지는 것을 관찰했습니다.

현상의 원리:

• 각 메트로놈의 진동이 공통 받침대(나무 판자)를 통해 다른 메트로놈에 미세한 진동을 전달
• 이러한 약한 결합(Weak Coupling)을 통해 상호 영향을 주고받음
• 에너지 효율성에 의해 결국 모든 메트로놈이 같은 위상으로 동조
• 개별 제어 없이 자발적으로 나타나는 창발적(Emergent) 현상

쿠라모토 모델 (Kuramoto Model)

1975년 일본의 물리학자 쿠라모토 요시키(Yoshiki Kuramoto)가 제안한 수학 모델로, 결합된 진동자들의 동기화 현상을 설명하는 대표적인 이론입니다.

기본 방정식:

1dθᵢ/dt = ωᵢ + (K/N) Σⱼ₌₁ᴺ sin(θⱼ - θᵢ)

변수 설명:

• θᵢ: i번째 진동자의 위상
• ωᵢ: i번째 진동자의 고유 진동수 (자연 리듬)
• K: 결합 강도 (상호작용의 세기)
• N: 진동자의 총 개수

핵심 개념:

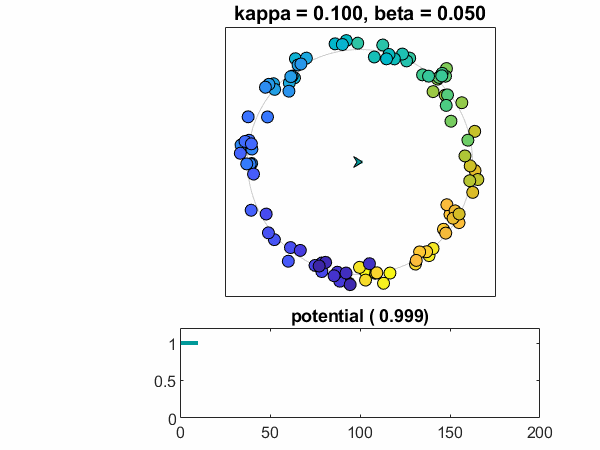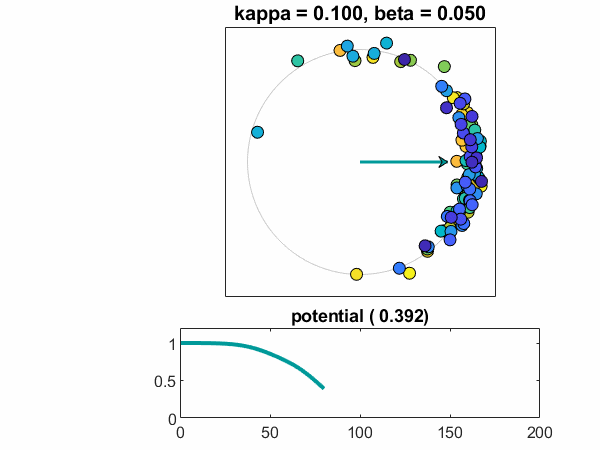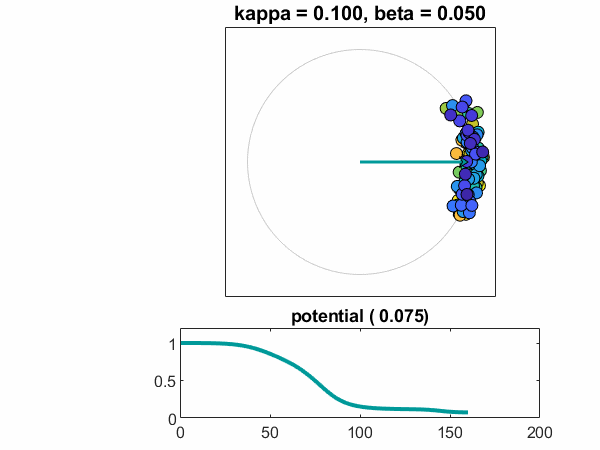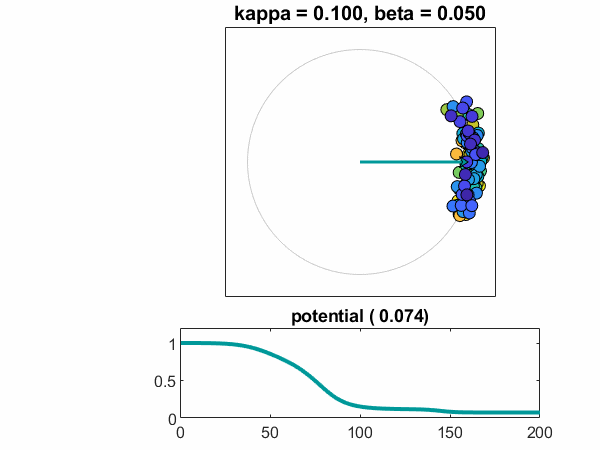
임계점 (Critical Point): 결합 강도 K가 임계값 Kc를 넘으면 부분적 동기화 상태로 급격히 전이

• K < Kc: 비동기 상태 (각자 제멋대로)
• K > Kc: 부분 동기화 상태 (점진적 조화)

• K >> Kc: 완전 동기화 상태 (완벽한 조화)

질서 매개변수 (Order Parameter):

• r = 0: 완전 비동기 상태
• 0 < r < 1: 부분 동기화 상태

• r = 1: 완전 동기화 상태

1r = |1/N Σⱼ₌₁ᴺ e^(iθⱼ)|

위상 전이 (Phase Transition): 임계점에서 질적으로 다른 상태로의 급격한 변화

실제 응용 분야:

• 생물학: 심장 박동 조율세포, 뇌 신경세포 집단 진동, 반딧불이 동기화 발광
• 물리학: 레이저 배열 동기화, 조세프슨 접합 배열, 화학 진동자
• 공학: 전력망 동기화, 센서 네트워크 시간 동기화, 로봇 군집 제어
• 사회과학: 박수갈채 동기화, 경제 시스템 동조화, 사회적 합의 형성

모델의 의의:
쿠라모토 모델은 복잡한 집단 동역학을 간단한 수학적 틀로 설명할 수 있어, 물리학을 넘어 생물학, 사회학, 경제학 등 다양한 분야에서 집단 행동과 창발 현상을 이해하는 핵심 도구로 활용되고 있습니다. 특히 개별 요소들의 상호작용이 어떻게 전체 시스템의 질적 변화를 이끌어내는지를 수학적으로 증명한 점에서 현대 복잡계 과학의 기초 이론으로 평가받고 있습니다.

Sample Code:

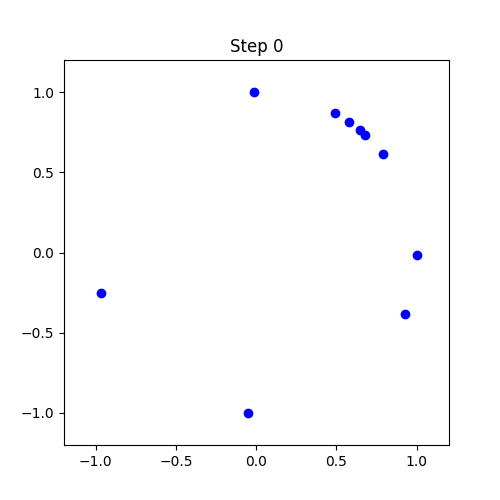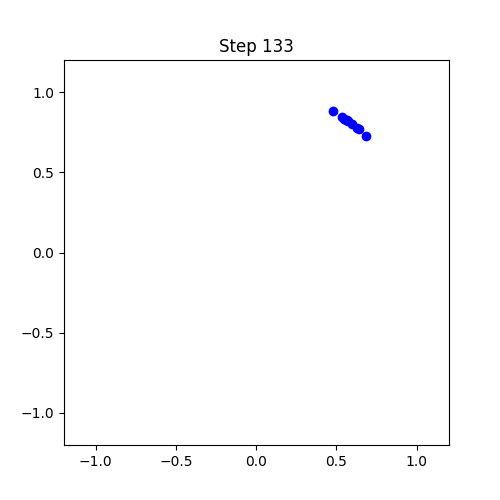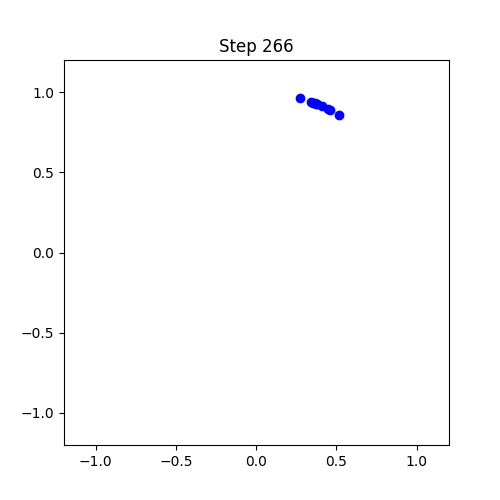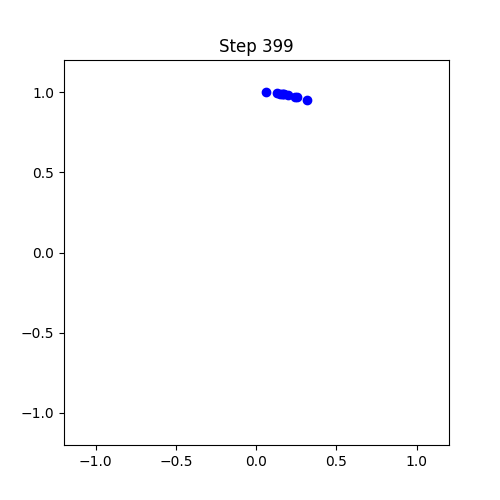
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation

# GIF 저장을 위한 Pillow 백엔드 설정
from matplotlib import rc
rc('animation', html='html5')

# 진동자 수와 시간 설정
N = 10       # 진동자 수
T = 20       # 총 시뮬레이션 시간 (초)
dt = 0.05    # 시간 간격
steps = int(T / dt)

# 초기 위상과 고유 진동수
theta = np.random.uniform(0, 2*np.pi, N)
omega = np.random.normal(loc=1.0, scale=0.1, size=N)

# 결합 강도
K = 1.5

# 위상 기록
theta_history = np.zeros((steps, N))

# 시뮬레이션 수행
for t in range(steps):
    theta_history[t] = theta
    dtheta = np.zeros(N)
    for i in range(N):
        coupling = np.sum(np.sin(theta - theta[i]))
        dtheta[i] = omega[i] + (K / N) * coupling
    theta += dtheta * dt

# 애니메이션 생성
fig, ax = plt.subplots(figsize=(5, 5))
ax.set_xlim(-1.2, 1.2)
ax.set_ylim(-1.2, 1.2)
ax.set_aspect('equal')
dots, = ax.plot([], [], 'o', color='blue')
title = ax.set_title("Kuramoto Model")

def update(frame):
    angles = theta_history[frame]
    x = np.cos(angles)
    y = np.sin(angles)
    dots.set_data(x, y)
    title.set_text(f"Step {frame}")
    return dots, title

ani = animation.FuncAnimation(fig, update, frames=steps, interval=50, blit=True)

# === GIF 저장 ===
ani.save("kuramoto_simulation.gif", writer="pillow", fps=20)
print("GIF 저장 완료: kuramoto_simulation.gif")