인공지능에서 수학의 필요성과 수학적 기초 (상세 편)
안녕하세요! 이전 포스트에서 AI의 기본 수학적 기초를 소개했는데요, 이번에는 더 구체적으로 각 분야를 깊이 파고 들어보겠습니다. 사용자가 제안해주신 주제들을 중심으로 설명하겠습니다. AI는 수학 없이 표면적으로만 사용할 수 있지만, 진짜 이해와 혁신은 수학에서 나옵니다.
아래는 AI/머신러닝에서 핵심적인 수학 분야의 개요 다이어그램입니다.
아래는 AI/머신러닝에서 핵심적인 수학 분야의 개요 다이어그램입니다.


1. 신경망에서의 선형대수 (Linear Algebra in Neural Networks)
신경망의 기본 건물 블록은 벡터, 행렬, 텐서입니다. 입력 데이터, 가중치, 출력이 모두 이러한 구조로 표현되며, 층 간 변환은 행렬 곱셈으로 이루어집니다.
주요 개념:
- 벡터: 데이터 포인트 표현
- 행렬: 선형 변환 (e.g., fully connected layer: y = Wx + b)
- 텐서: 고차원 데이터 (e.g., 이미지: 배치 × 채널 × 높이 × 너비)
- 추가: 고유값 분해 (Eigen decomposition), SVD (특이값 분해) – PCA, 차원 축소에 사용
아래 이미지는 벡터, 행렬, 텐서의 관계와 신경망에서의 역할을 보여줍니다.

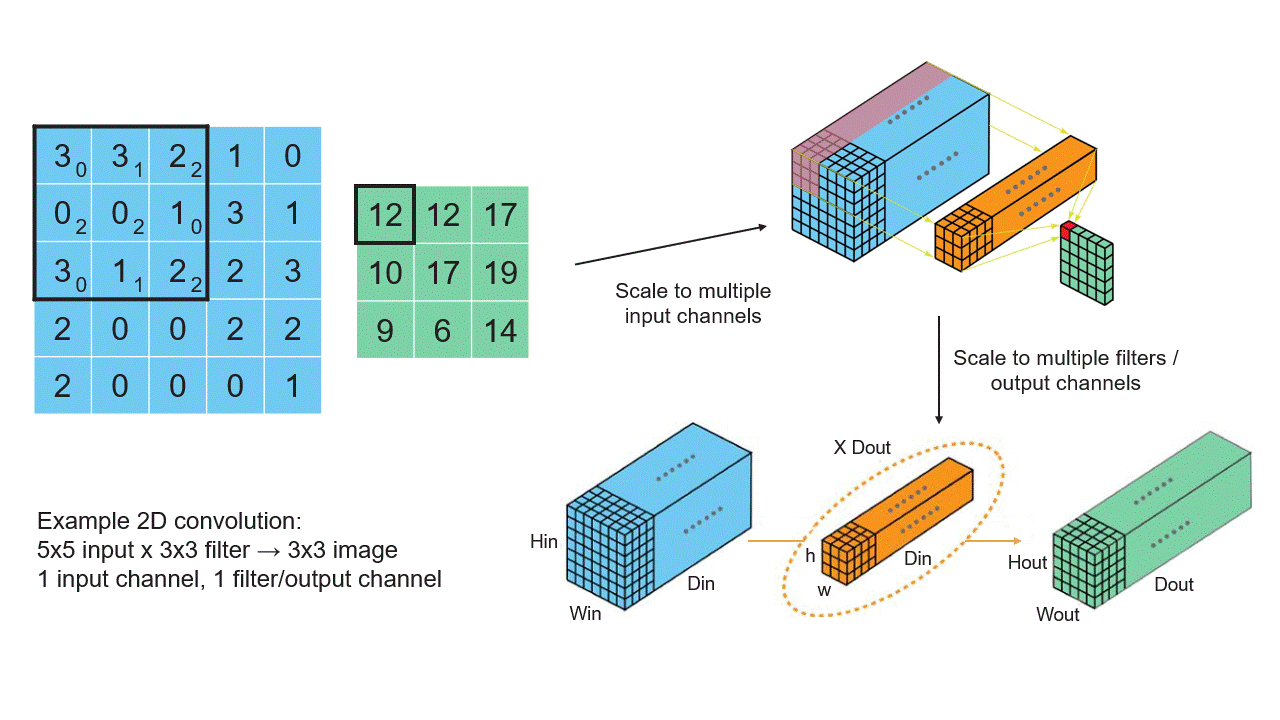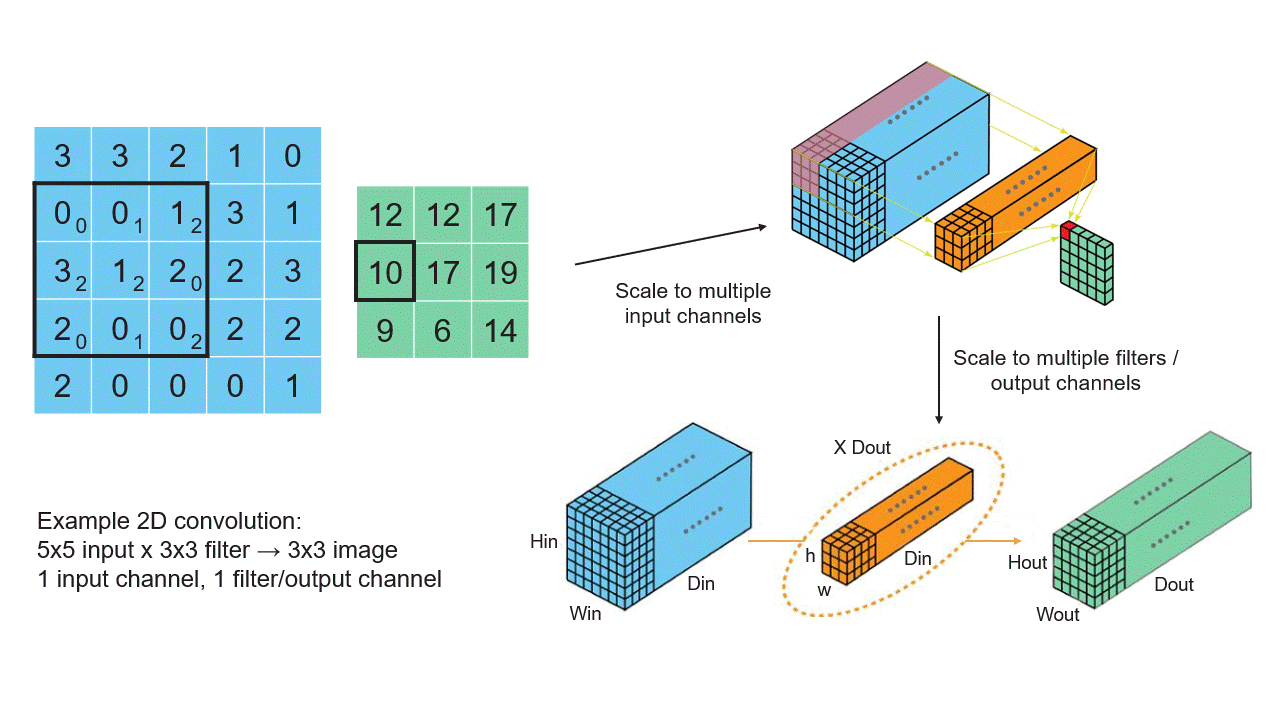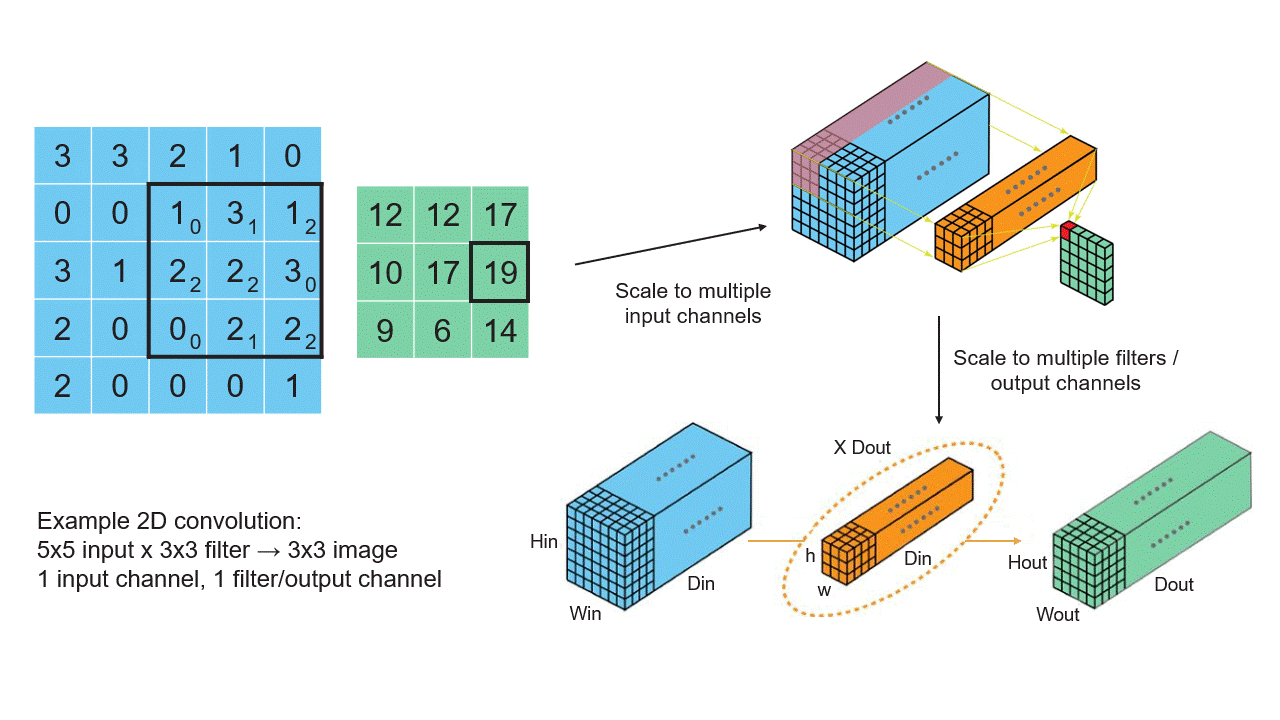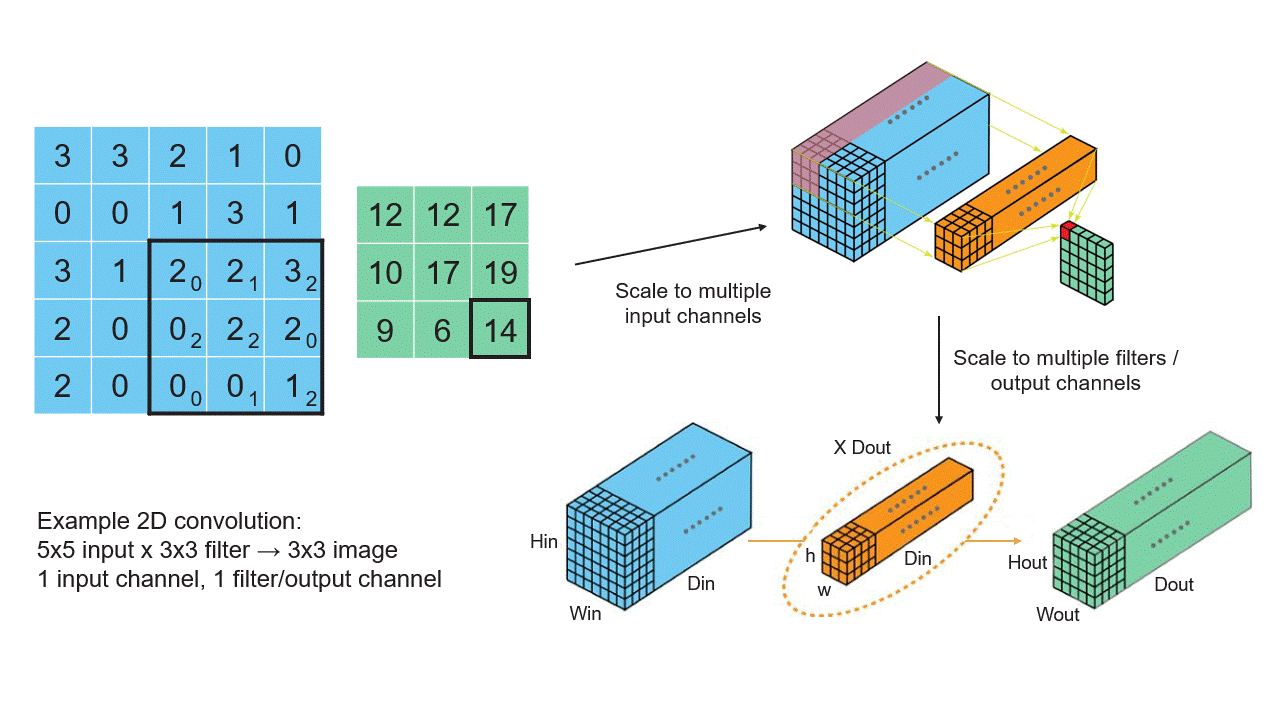

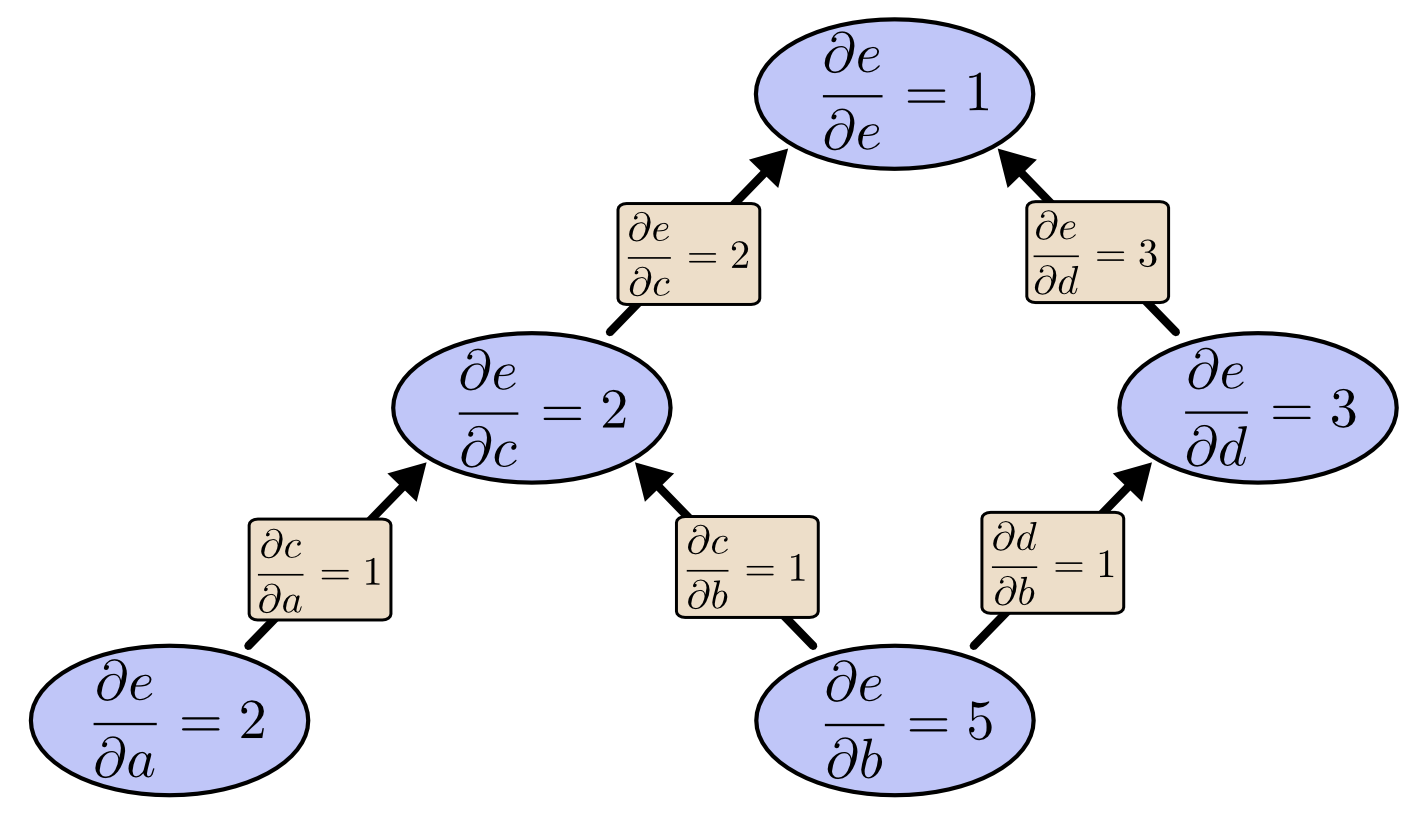
2. 역전파에서의 미적분학 (Calculus in Backpropagation)
역전파(backpropagation)는 신경망 학습의 핵심으로, 손실 함수의 기울기(gradient)를 계산해 파라미터를 업데이트합니다. 이는 미적분의 chain rule에 기반합니다.
주요 개념:
- 미분/편미분: 손실 함수 L에 대한 가중치 w의 기울기 ∂L/∂w
- Chain rule: 다층 네트워크에서 기울기 전파
- Gradient Descent: θ ← θ - η ∇L(θ)
아래 다이어그램은 역전파 과정과 chain rule을 시각화합니다.


3. 의사결정에서의 확률 (Probability in Decision Making)
AI에서 확률은 불확실한 상황에서의 의사결정을 가능하게 합니다. 베이지안 추론(Bayesian inference)이 대표적입니다.
주요 개념:
- 조건부 확률, 베이즈 정리: P(A|B) = P(B|A)P(A)/P(B)
- 확률적 모델: 나이브 베이즈, 베이지안 네트워크
- 의사결정 트리나 강화학습에서 기대값 최대화
![Bayesian Network Made Simple [How It Is Used In AI & ML]](https://spotintelligence.com/wp-content/uploads/2024/02/bayesian-netowork-node-edges.jpg)

4. 통계학 (데이터를 통해 배우기) (Statistics in Learning from Data)
통계는 데이터를 분석하고 모델을 평가하는 데 필수입니다. 머신러닝은 데이터 분포를 추정하고 일반화합니다.
주요 개념:
- 확률 분포 (정규분포 등)
- 가설 검정 (Hypothesis testing), p-value
- 추정: 최대우도추정 (MLE), MAP

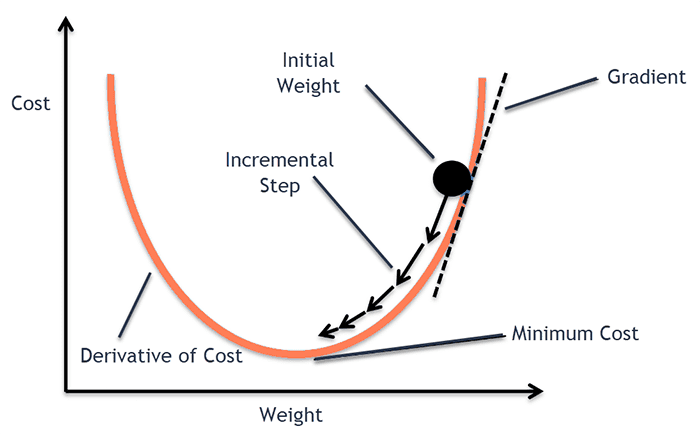
5. 훈련 최적화 (Training Optimization)
손실 함수의 최소점을 찾는 과정으로, convex/non-convex 최적화가 포함됩니다.
주요 개념:
- Gradient Descent 변형 (SGD, Adam 등)
- Loss landscape: saddle point, local minima


6. 정보 이론 (Information Theory)
정보를 정량화해 모델의 효율성을 높입니다. 특히 엔트로피와 크로스 엔트로피가 손실 함수로 사용됩니다.
주요 개념:
- 엔트로피 H(p) = -∑ p log p
- KL 발산, Mutual Information
- 크로스 엔트로피 손실: 분류 문제에서 사용
7. 이산수학 및 논리 (Discrete Mathematics & Logic)
그래프 기반 모델, 지식 표현, 논리 추론에 사용됩니다.
주요 개념:
- 그래프 이론: Knowledge Graph, GNN
- 논리: Prolog 스타일 추론, Boolean algebra
- 조합론: 알고리즘 복잡도
![Knowledge Graph Reasoning Made Simple [3 Technical Methods]](https://i0.wp.com/spotintelligence.com/wp-content/uploads/2024/02/query2vec.jpg?fit=1200%2C675&ssl=1)
마무리
이 분야들을 하나씩 공부하면 AI 논문을 읽고, 모델을 직접 개선할 수 있게 됩니다. 추천: "Mathematics for Machine Learning" 책이나 Khan Academy/3Blue1Brown 영상!
더 궁금한 부분 있으시면 댓글 달아주세요. 수학으로 AI를 정복합시다!
(본 자료는 Grok과 대화로 만든 자료입니다)
